物理类

Pulay方法

或者名为DIIS(direct inversion of the iterative subspace)。 原始公式为： $p_{n+1}=\sum^n_{i=1}{c_ip_i}$ 实际上一般还需要加上线性混合： $p_{n+1}=\sum^n_{i=1}{c_i[\beta p_{i,in}+(1-\beta)p_{i,out}]}$ 系数$c_i$由以下线性方程来解： $\left( \begin{array}{cccc} 0&-1&...&-1\\ -1&b_{11}&...&b_{1n}\\ ...&...&...&...\\ -1&b_{n1}&...&b_{nn} \end{array} \right) \left( \begin{array}{c} \lambda\\c_{1}\\...\\c_{n} \end{array} \right)= \left( \begin{array}{c} -1\\0\\...\\0 \end{array} \right)$ 其中$b_{i,j}=Real(<\Delta p_i,\Delta p_j>), \Delta p_i = p_{i+1}-p_{i}$。

Gap Function的对称性

$s$-wave： $\Delta(-k_x, k_y) = \Delta(k_x, -k_y) = \Delta(k_x, k_y), \Delta(k_x, k_y) = \Delta(k_y, k_x)$ $d_{x^2-y^2}$-wave： $\Delta(-k_x, k_y) = \Delta(k_x, -k_y) = \Delta(k_x, k_y), \Delta(k_x, k_y) = -\Delta(k_y, k_x)$ $d_{xy}$-wave： $\Delta(-k_x, k_y) = \Delta(k_x, -k_y) = -\Delta(k_x, k_y), \Delta(k_x, k_y) = \Delta(k_y, k_x)$ $g$-wave： $\Delta(-k_x, k_y) = \Delta(k_x, -k_y) = -\Delta(k_x, k_y), \Delta(k_x, k_y) = -\Delta(k_y, k_x)$

线性Eliashberg方程的求解

$\lambda\Delta_{lm}(k)=-\frac{T}{N}V_{ll'',m''m}^{S}(k-k')G_{l''l'}(k')G_{m''m'}(-k')\Delta_{l'm'}(k')$

该方程本身高度非线性，不要被名字骗了，如果只要求解最大特征值，可以通过幂法求解，类似于求解一个矩阵最大特征值。

伪代码（Fortran风格）：

u=v
while not converge do
    v=Au
    lambda1=abs_max(v)
    u=v/lambda1
end

能带展开的方法

通过实空间中Wannier函数的对称性展开，去掉一些重复的量。 $Fe_1-1\ to\ Fe_2-1,\ corresponds\ 1\ to\ 6;$ $Fe_1-1\ to\ Fe_2-2,\ corresponds\ 1\ to \ 7;$ $...$

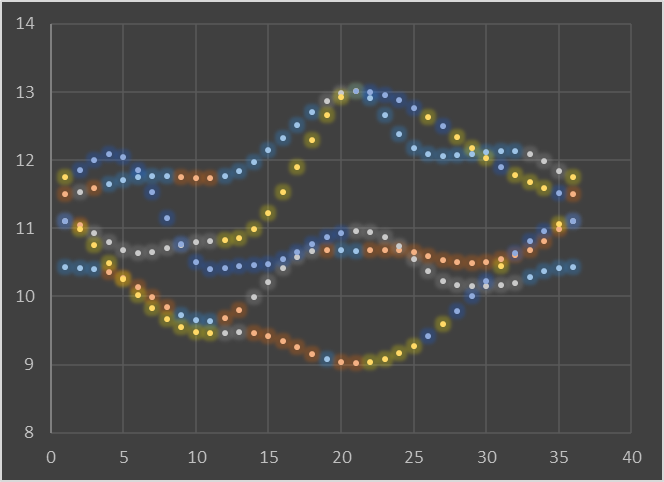
将实空间中的Wannier函数变换到展开布里渊区中，在每一个$k$点上对一个5*5矩阵进行对角化，得到能带能量的本征值。

一个较好的展开结果如下图：